EPPS Math and Coding Camp

Preliminaries

Instructor: Prajyna Barua

SETS

• a set is just a collection of elements,

• groups whose members have something in common that is important to the person who has grouped them together.

Example:
(0, 1, 2, …,where … signifies that this progression goes on indefinitely) belong to the set of natural numbers.

• The set of all natural numbers is denoted N, and any variable \(n\) that is a natural number must come from this set.

• If we add negative numbers to the set of natural numbers, i.e., …, -3, -2, -1, then we get the set of all integers, denoted Z.

• All numbers that can be expressed as a ratio of two integers are called rational numbers, and the set of these is denoted Q.

• The set of all rational and irrational numbers together is known as the real numbers and is denoted R.

Notation	Meaning
N	Natural numbers
Z	Integers
Q	Rational numbers
R	Real (rational and irrational) numbers
C	Complex numbers
Subscript: N+	Positive (negative) values of the set
Superscript: Nd	Dimensionality (number of dimensions)

• Z₊, the set of all positive integers, which is a subset of all integers.

• Continuous variables are those whose values cannot each be assigned a single integer.

• We typically assume that continuous variables are drawn from a subset of the real numbers, though this is not necessary.

Example:
The set of solutions to the equation \(x^2 - 5x + 6 = 0\) is \(\{2, 3\}\), a discrete set.

• We term a sample space a set that contains all of the values that a variable can take in the context of statistical inference.

• More generally, the superscript indicates the dimensionality of the space.

• We will frequently use the \(d\)-dimensional space R^d in this book. When \(d=3\), this is called Euclidean space

• Ordered pair, written \((a,b)\). Unlike elements of R³, in which each of \(x, y\), and \(z\) is a real number, each member of an ordered pair may be quite different

• Ordered pairs are often formed via Cartesian products.

• A countable set is one whose elements can be counted, i.e., each one can be associated with a natural number (or an integer).

• An uncountable set does not have this property.

• A bounded set has finite size while an unbounded set does not.

• We say a set has a lower bound if there is a number, \(u\), such that every element in the set is no smaller than it, and an upper bound if there is a number, \(v\), such that every element in the set is no bigger than it.

• The greatest lower bound is the largest such lower bound, and the least upper bound is the smallest such upper bound.

• \(x \in A\) states that “\(x\) is an element of the set \(A\)” or “\(x\) is in \(A\).”

• \(x \in \{1, 2, 3\} \text{ or } x \in [0, 1]\) means \(x\) can take the value \(1, 2,\) or \(3\), or \(x\) can be any real number from \(0\) to \(1\), inclusive.

• \(y \in \{0, 1\}\) means that \(y\) either can take a value of \(0\) or a value of \(1\).

• We use the symbol \(\notin\) as in \(x \notin A\). This means that, for the examples in the previous paragraph, \(x\) does not take the values 1, 2, or 3 or is not between 0 and 1.

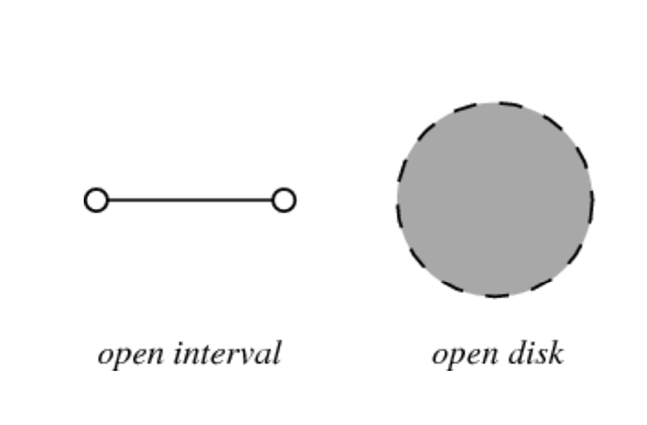
• Continuous sets use square brackets or parentheses depending on whether they are closed or open, e.g.\([0,1]\) or \((0,1)\)

• The expression \(A \subset B\) (read ‘\(A\) is a proper subset of \(B\)’) implies that set \(B\) contains all the elements in \(A\), plus at least one more. More formally if all \(x\) that are elements in \(A\) are also elements in \(B\).

• A universal set contains all elements.

• Ordered set: The order of elements matters.
  • Example: {a, b, c} ≠ {b, a, c}

• Unordered set: The order does not matter.
  • Example: {a, b, c} = {c, b, a}

4.3 OPEN,CLOSED,COMPACT,ANDCONVEXSETS

• An open set is one in which there is some distance (which may be arbitrarily small) that you may move in any direction within the set and stay in the set.

• A closed set is one that contains all its limit points.

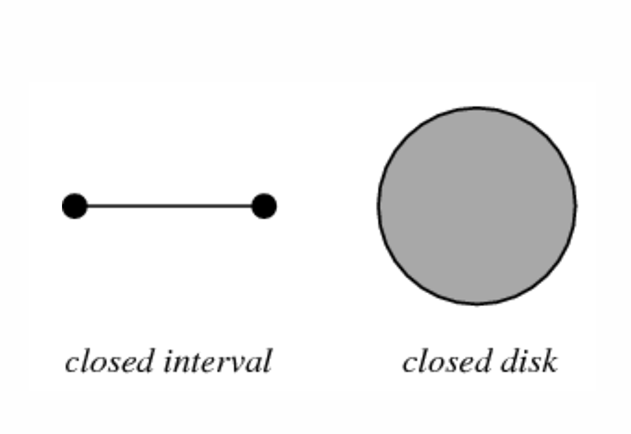
• A set that is not closed, in contrast, can have the point the sequence approaches — the set’s limit point — outside the set, even if all prior points in the sequence are in the set.

• The set contains all its limit points and can itself be contained within some finite boundary—is called compact.

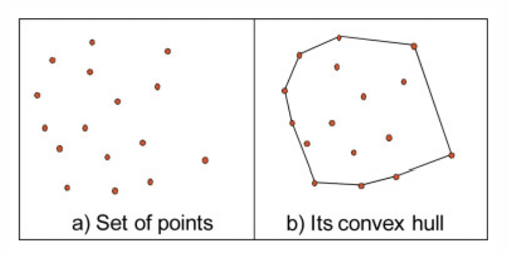
• A subset of Rⁿ for which every pair of points in the set is joined by a straight line that is also in the set is called a convex set. Formally, a set is convex if for all points \(x\) and \(y\) in it and all \(\lambda \in [0,1]\), the point \((1-\lambda)x+\lambda y\) is also in the set.

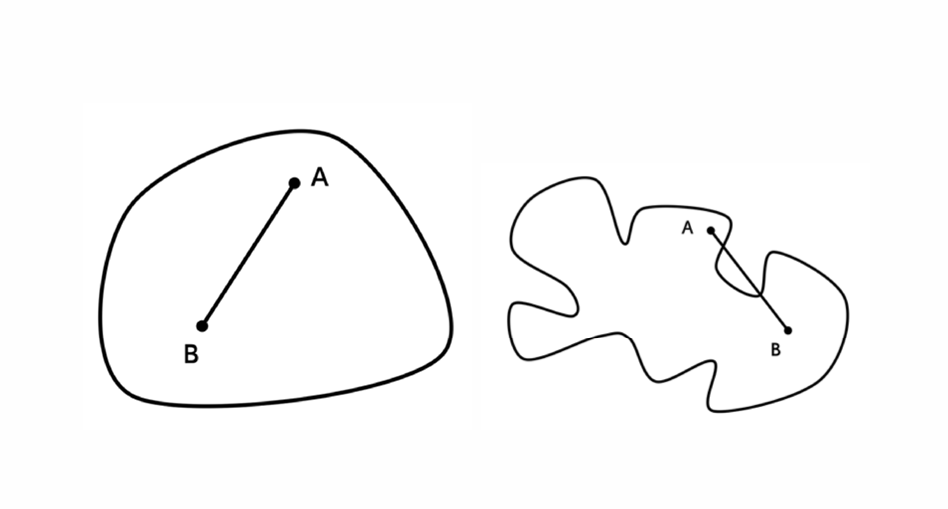
• The convex hull of a set \(A\) is the set \(A\) plus all the points needed to make A convex.

Operators:

\[+, -, \times, /, x^n, \sqrt[n]{x}, \sum, \prod, !\]

• product operator:

\[ \prod_{i=k}^{l} x_i = x_k \times \ldots \times x_l \]

• Summation operator:

\[ \sum_{i=k}^{l} x_i = x_k + \ldots + x_l \]

• Relations: \(<, \leq,=,\geq, >, \neq\)

• Exponential and Roots:

• \(x^n\): Exponentiation

• \(\sqrt[n]{x}\): nth Root

• \(n!\): Factorial

• \(5! = 5 \times 4 \times 3 \times 2 \times 1 = 120\)

• Operators on Sets:

• Difference:
• \[ x \in (A \setminus B) \iff x \in A \ \text{and} \ x \notin B \]

• Complement:
• \[ x \in A^c \] contains elements not in A

• Intersection:
• \[ x \in A \cap B \iff (x \in A )\ and\ ( x \in B ) \] elements common to both A and B

• Union:
• \[ x \in A \cup B \iff (x \in A )\ or\ ( x \in B ) \] elements in either A or B

• Mutually Exclusive Sets:
• \[ x \in A \cap B = \emptyset \] If elements in A than not in B and vice versa

• Partition: A collection of subsets whose union forms the set.

Example:
\[ A = \{\text{Bush, Kerry, Nader}\}\]
Possible partitions:
\[\{\{Bush\}, \{Kerry\}, \{Nader\}\}\]
\[ \{\{Bush, Kerry\}, \{Nader\}\}\] or any similar combinations

• The Cartesian product is the set of cardinality four consisting of all possible ordered pairs:
  

\[A=\{\text{Female, Male}\} \\ B=\{\text{Income over \$50k, Income under \$50k}\}\]

\[A \times B =\\ \{(\text{Female, Income over \$50k}), \\ (\text{Female, Income udner \$50k}), \\ (\text{Male, Income over \$50k}), \\ (\text{Male, Income under \$50k})\}\]

1.4 RELATIONS

• A binary relation can be represented as an ordered pair.

So, if \(a \in A\) is greater than \(b \in A\), we can write the relation as \((a, b)\)

• If a function transforms an element of \(A\) into an element of \(B\), we call \(A\) the domain and \(B\) the range.

Summary of Symbols and Notation

Symbol	Meaning
\(+\)	Addition
\(-\)	Subtraction
\(*\) or \(x\) or \(\cdot\)	Multiplication
\(/\) or \(\div\)	Division
\(\pm\)	Plus or minus
\(x^n\)	Exponentiation (“to the nth power”)
\(\sqrt[n]{x}\)	Radical or nth root
\(!\)	Factorial
\(\infty\)	Infinity
\(\sum_{i=k}^l x_i\)	Sum of \(x_i\) from index \(i=k\) to \(i=l\)
\(\prod_{i=k}^l x_i\)	Product of \(x_i\) from index \(i=k\) to \(i=l\)
\(\ldots\)	Continued progression

Symbol	Meaning
\(\frac{d}{dx}\)	Total derivative with respect to \(x\)
\(\frac{\delta}{\delta x}\)	Partial derivative with respect to \(x\)
\(\int dx\)	Integral over \(x\)
\(\cup\)	Set union
\(\cap\)	Set intersection
\(\times\)	Cartesian product of sets
\(\setminus\)	Set difference
\(A^c\)	Complement of set \(A\)
\(\emptyset\)	Empty (or null) set
\(\in\)	Set membership
\(\notin\)	Not member of set
\(\vert\) or \(:\) or \(\ni\)	Such that
\(\subset\)	Proper subset
\(\subseteq\)	Subset

Symbol	Meaning
\(<\)	Less than
\(\leq\)	Less than or equal to
\(=\)	Equal to
\(>\)	Greater than
\(\geq\)	Greater than or equal to
\(\neq\)	Not equal to
\(\equiv\)	Equivalent to or Defined as
\(f(x)\) or \(f(\cdot)\)	Function

Symbol	Meaning
\(\{\) \(\}\)	Delimiter for discrete set
\((\) \()\)	Delimiter for open set
\([\) \(]\)	Delimiter for closed set
\(\forall\)	For all (or for every or for each)
\(\exists\)	There exists
\(\Rightarrow\)	Implies
\(\Leftrightarrow\)	If and only if
\(\neg\) or \(\sim\)	Negation (not \(C\))

Greek Letters

Upper-case	Lower-case	English	Upper-case	Lower-case	English
\(A\)	\(\alpha\)	alpha	\(N\)	\(\nu\)	nu
\(B\)	\(\beta\)	beta	\(\Xi\)	\(\xi\)	xi
\(\Gamma\)	\(\gamma\)	gamma	\(O\)	\(o\)	omicron
\(\Delta\)	\(\delta\)	delta	\(\Pi\)	\(\pi\)	pi
\(E\)	\(\epsilon\)	epsilon	\(P\)	\(\rho\)	rho
\(Z\)	\(\zeta\)	zeta	\(\Sigma\)	\(\sigma\)	sigma
\(H\)	\(\eta\)	eta	\(T\)	\(\tau\)	tau
\(\Theta\)	\(\theta\)	theta	\(\Upsilon\)	\(\upsilon\)	upsilon
\(I\)	\(\iota\)	iota	\(\Phi\)	\(\phi\)	phi
\(K\)	\(\kappa\)	kappa	\(X\)	\(\chi\)	chi
\(\Lambda\)	\(\lambda\)	lambda	\(\Psi\)	\(\psi\)	psi
\(M\)	\(\mu\)	mu	\(\Omega\)	\(\omega\)	omega

Problems

Problem 1

Given the sets \(S_1 = \{2, 4, 6\}\), \(S_2 = \{7, 2, 6\}\), \(S_3 = \{4, 2, 6\}\), and \(S_4 = \{2, 4\}\), which of the following statements are true?

1. \(S_1 = S_3\)

2. \(S_1 = \mathbb{R}\) (set of real numbers)

3. \(8 \in S_2\)

4. \(3 \notin S_2\)

5. \(4 \notin S_3\)

6. \(S_4 \subset \mathbb{R}\)

7. \(S_1 \supset S_4\)

8. \(\emptyset \subset S_2\)

9. \(S_3 \supset \{1, 2\}\)

Problem 2

Referring to the four sets given in Problem 1, find:

1. \(S_1 \cup S_2\)

2. \(S_1 \cup S_3\)

3. \(S_2 \cap S_3\)

4. \(S_2 \cap S_4\)

5. \(S_4 \cap S_2 \cap S_1\)

6. \(S_3 \cup S_1 \cup S_4\)

Problem 3

Which of the following statements are valid?

1. \(A \cup A = A\)

2. \(A \cap A = A\)

3. \(A \cup \emptyset = A\)

4. \(A \cup U = U\)

5. \(A \cap \emptyset = \emptyset\)

6. \(A \cap U = A\)

7. The complement of \(A\) is \(A\)

Problem 4

Write an element of the Cartesian product \([0, 1) \times (1, 2)\).

Problem 5

Given \(S_1 = \{3, 6, 9\}\), \(S_2 = \{a, b\}\), and \(S_3 = \{m, n\}\), find the Cartesian products:

1. \(S_1 \times S_2\)

2. \(S_1 \times S_2 \times S_3\)

Any Questions?

Home